Sin 2 X Cos X

Trigonometry Formulas

Last updated at Oct. 8, 2021 past Teachoo

In Trigonometry Formulas, we will learn

• Basic Formulas

• sin, cos tan at 0, 30, 45, 60 degrees

• Pythagorean Identities

• Sign of sin, cos, tan in different quandrants

• Radians

• Negative angles (Even-Odd Identities)

• Value of sin, cos, tan repeats after 2π

• Shifting bending by π/2, π,  3π/ii (Co-Part Identities or Periodicity Identities)

• Angle sum and difference identities

• Double Angle Formulas

• Triple Angle Formulas

• Half Angle Identities (Power reducing formulas)

• Sum Identities (Sum to Product Identities)

• Product Identities (Product to Sum Identities)

• Law of sine

• Law of cosine

• What are Inverse Trigonometry Functions?

• Domain and range of Inverse Trigonometry Functions

• Inverse Trigonometric Formulas

• Changed Trigonometry Substitutions

Basic Formulas

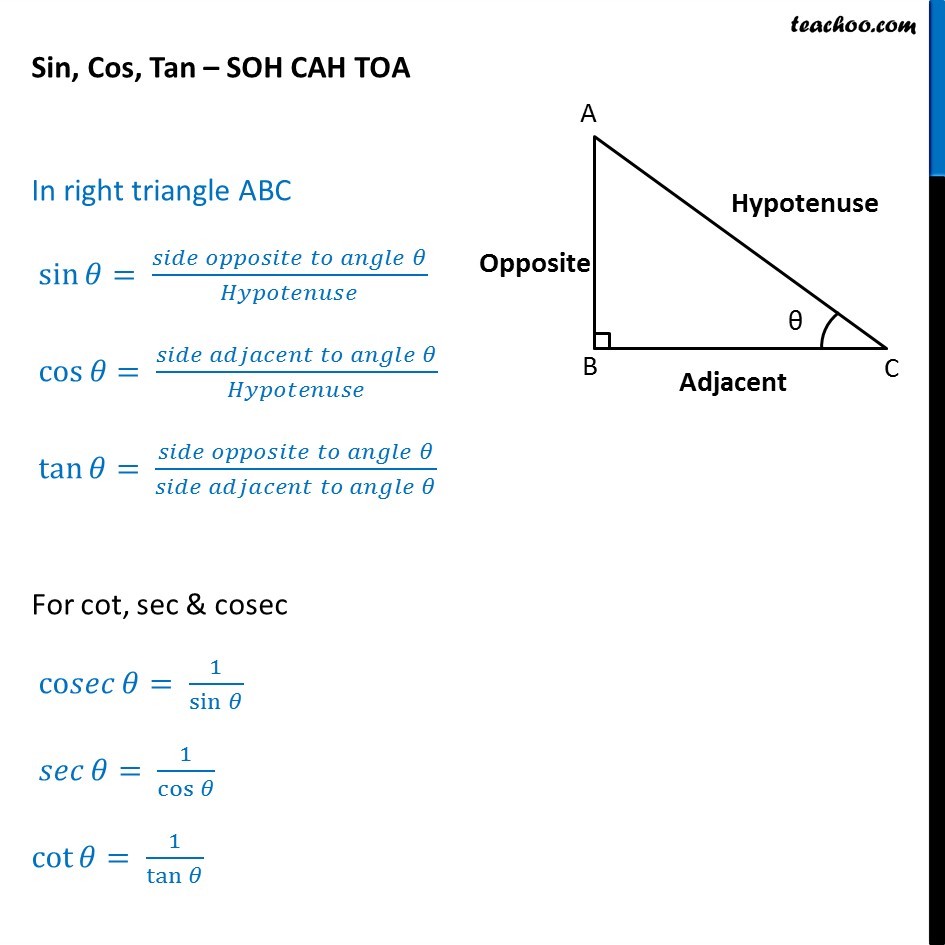
sin, cos tan at 0, thirty, 45, 60 degrees

Pythagorean Identities

Signs of sin, cos, tan in unlike quadrants

To learn sign of sin, cos, tan in dissimilar quadrants,

we remember

A dd → S ugar → T o → C offee

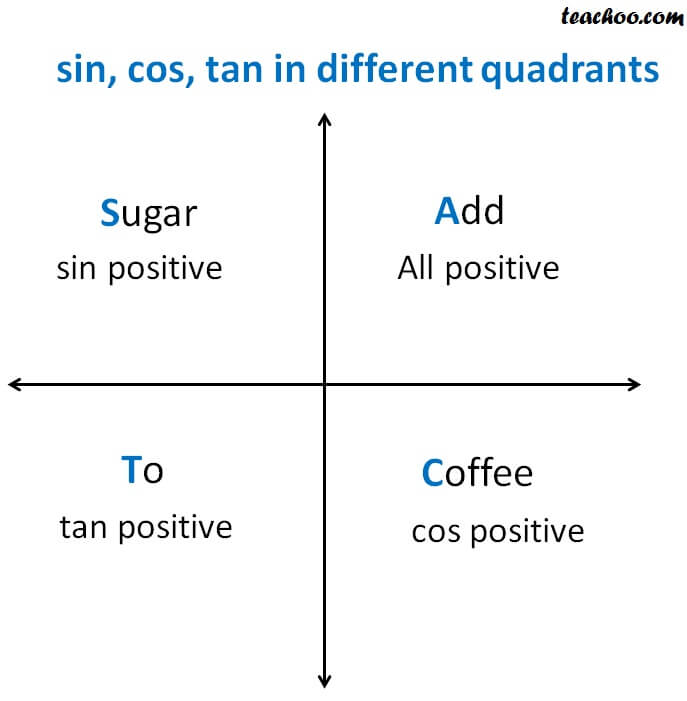
Representing as a table

	Quadrant I	Quadrant II	Quadrant III	Quadrant Four
sin	+	+	–	–
cos	+	–	–	–
tan	+	–	+	–

Radians

Radian measure = π/180  ×  Degree measure

Likewise,

i Degree = 60 minutes

i.e. ane° = 60'

1 Minute = 60 seconds

i.e. one' = lx''

Negative angles (Even-Odd Identities)

sin (–x) = – sin x

cos (–x) = cos x

tan (–ten) = – tan 10

sec (–ten) = sec ten

cosec (–x) = – cosec x

cot (–x) = – cot ten

Value of sin, cos, tan repeats after 2π

sin (2π + x) = sin x

cos (2π + x) = cos ten

tan (2π + x) = tan x

Shifting bending by π/2, π,  3π/2 (Co-Office Identities or Periodicity Identities)

sin (π/2 – 10) = cos ten	cos (π/two – x) = sin 10
sin (π/two + x) = cos x	cos (π/2 + x) = – sin x
sin (3π/two – x)  = – cos x	cos (3π/ii – x)  = – sin x
sin (3π/2 + x) = – cos ten	cos (3π/ii + 10) = sin x
sin (π – 10) = sin ten	cos (π – x) = – cos 10
sin (π + ten) = – sin ten	cos (π + x) = – cos ten
sin (2π – x) = – sin ten	cos (2π – x) = cos x
sin (2π + 10) = sin x	cos (2π + x) = cos x

Angle sum and departure identities

Double Angle Formulas

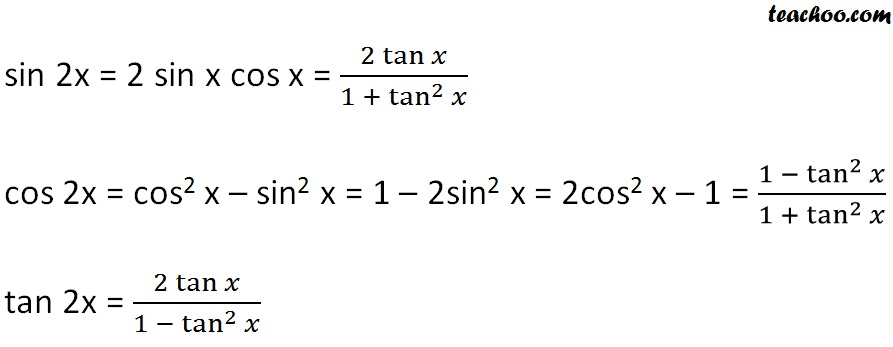
Triple Angle Formulas

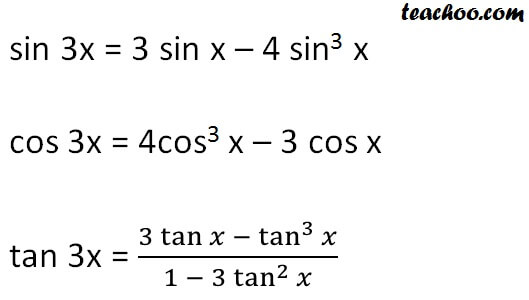
Half Angle Identities (Power reducing formulas)

Sum Identities (Sum to Product Identities)

Production Identities (Product to Sum Identities)

Production to sum identities are

2 cos⁡ten  cos⁡y = cos⁡ (x + y) + cos⁡(ten - y)

-2 sin⁡x  sin⁡y = cos⁡ (x + y) - cos⁡(x - y)

2 sin⁡10  cos⁡y = sin⁡ (x + y) + sin⁡(10 - y)

ii cos⁡x  sin⁡y = sin⁡ (x + y) - sin⁡(x - y)

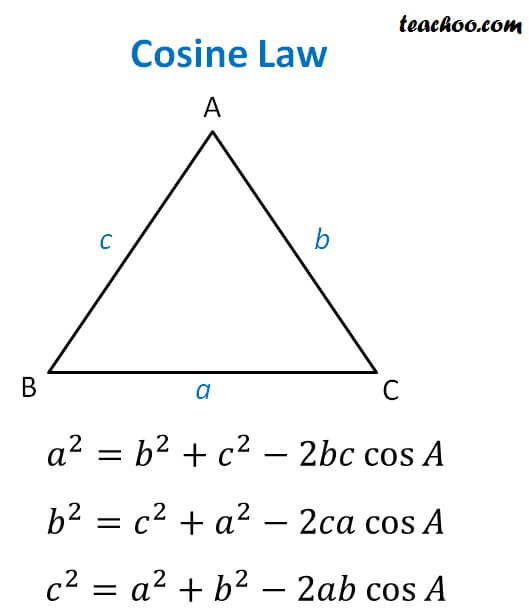
Police of sine

Here

• A, B, C are vertices of Δ ABC
• a is side opposite to A i.e. BC
• b is side opposite to B i.east. AC
• c is side opposite to C i.due east. AB

Law of cosine

Just like Sine Police force, we have cosine Law

What are Inverse Trigonometric Functions

If sin θ = x

Then putting sin on the correct side

θ = sin ^-one x

sin ^-ane x = θ

So, inverse of sin is an bending.

Similarly, inverse of all the trigonometry function is angle.

Note : Here angle is measured in radians, non degrees.

And then, nosotros have

sin ^-1 10

cos ^-1 x

tan ^-1 10

cosec ^-i x

sec ^-1 x

tan ^-1 x

Domain and Range of Inverse Trigonometric Functions

	Domain	Range
sin -one	[–1, ane]	[-π/2,π/2]
cos -1	[–i, ane]	[0,π]
tan -i	R	(-π/ii,π/ii)
cosec -ane	R – (–i, i)	[π/2,π/two] - {0}
sec -1	R – (–1, one)	[0,π]-{π/2}
cot -1	R	(0,π)

Changed Trigonometry Formulas

Some formulae for Inverse Trigonometry are

sin ^–1 (–x) = – sin ^-one x

cos ^–1 (–x) = π – sin ^-1 x

tan ^–i (–x) = – tan ^-ane x

cosec ^–i (–x) = – cosec ^-1 ten

sec ^–i (–x) = – sec ^-1 10

cot ^–1 (–x) = π – cot ^-one 10

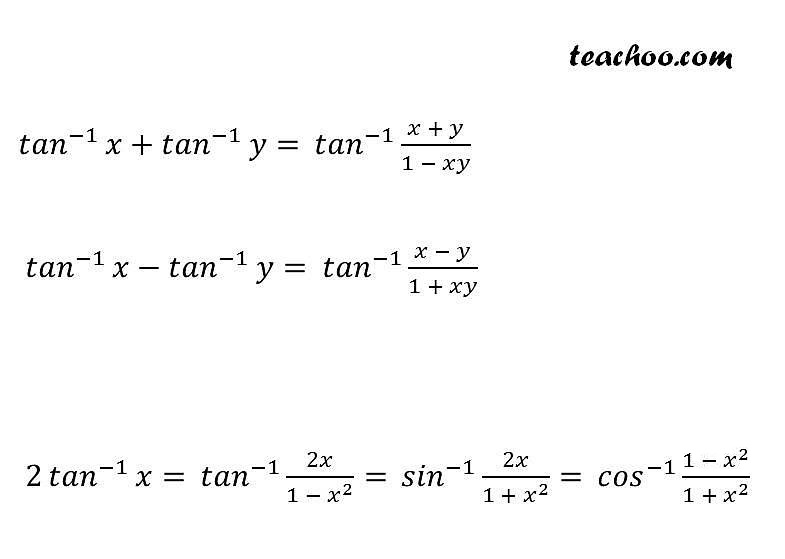
Inverse Trigonometry Substitution

Support Teachoo in making more (and meliorate content) - Monthly, half-dozen monthly, yearly packs bachelor!

Sin 2 X Cos X,

Source: https://www.teachoo.com/9723/1412/Trigonometry-Formulas/category/2-sin-x-sin-y-formula/

Posted by: broughtonthir1999.blogspot.com

Share this post